W analizie danych często spotykamy się z potrzebą oceny zmienności w zestawach danych. Jednym z kluczowych narzędzi do tego celu jest odchylenie standardowe. W tym artykule przyjrzymy się temu pojęciu bardziej szczegółowo, omówimy wzór na jego obliczanie oraz zastosowania praktyczne. Dowiedzmy się, jak to narzędzie może pomóc w lepszym zrozumieniu rozkładu danych.
Odchylenie Standardowe: Podstawowe Pojęcie
Odchylenie standardowe to miara rozproszenia danych wokół średniej wartości. Oznacza to, że informuje nas o tym, jak bardzo dane punkty różnią się od wartości średniej. Im większe odchylenie standardowe, tym większa zmienność danych, a im mniejsze – tym mniejsza zmienność.
Wzór na obliczanie odchylenia standardowego jest stosunkowo prosty:
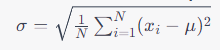
gdzie:
- σ to odchylenie standardowe,
- N to liczba obserwacji w zestawie danych,
- xi to pojedyncza obserwacja,
- μ to średnia wartość w zestawie danych.
Zastosowania Odchylenia Standardowego
Odchylenie standardowe ma wiele praktycznych zastosowań w analizie danych. Oto kilka z nich:
- Ocena stabilności procesu produkcyjnego: Przemysł często stosuje odchylenie standardowe do oceny stabilności procesu produkcyjnego. Im mniejsze odchylenie, tym bardziej stabilny proces, co przekłada się na niższą liczbę wad i lepszą jakość produktu.
- Analiza ryzyka inwestycyjnego: W finansach odchylenie standardowe jest używane do pomiaru ryzyka inwestycji. Wyższe odchylenie standardowe oznacza większe ryzyko, ponieważ dane inwestycje są bardziej zmienne.
- Medycyna i nauki przyrodnicze: Odchylenie standardowe jest również używane w badaniach naukowych, zwłaszcza w medycynie. Pomaga określić, jak bardzo wyniki badań różnią się od średnich wartości, co może prowadzić do ważnych odkryć.
Odchylenie Standardowe w Praktyce: Przykład
Aby lepiej zrozumieć, jak działa odchylenie standardowe, przyjrzyjmy się przykładowi. Załóżmy, że analizujemy wyniki testów z matematyki w klasie 8a. Nasze dane to punkty zdobyte przez każdego ucznia w teście. Chcemy ocenić, jak dobrze uczniowie poradzili sobie w teście i jakie jest odchylenie standardowe tych wyników.
Nasze dane wyglądają następująco:
- Uczeń A: 85 punktów
- Uczeń B: 92 punkty
- Uczeń C: 78 punktów
- Uczeń D: 88 punktów
- Uczeń E: 95 punktów
Średnia wartość wyników wynosi μ=85+92+78+88+955=87.6μ=585+92+78+88+95=87.6.
Teraz możemy obliczyć odchylenie standardowe, korzystając ze wzoru: σ= pierwiastek z 1/5[(85−87.6)2+(92−87.6)2+(78−87.6)2+(88−87.6)2+(95−87.6)2]σ=51[(85−87.6)2+(92−87.6)2+(78−87.6)2+(88−87.6)2+(95−87.6)2]
Po obliczeniach otrzymujemy wartość odchylenia standardowego równą 5.31.
To oznacza, że wyniki testów różnią się od średniej wartości średnio o 5.31 punktów. Im większe odchylenie standardowe, tym większa była by różnica między wynikami uczniów.
Odchylenie standardowe jest ważnym narzędziem analizy danych, które pomaga nam zrozumieć, jak zmienne są nasze dane. Jest używane w wielu dziedzinach, od przemysłu po nauki przyrodnicze. Dzięki niemu możemy oceniać stabilność procesów, mierzyć ryzyko inwestycji i prowadzić badania naukowe. Warto zapoznać się z tym pojęciem i umiejętnie stosować je w praktyce, aby lepiej zrozumieć i analizować dane, z którymi mamy do czynienia.



