W codziennym życiu często mierzymy i analizujemy różne odległości, niezależnie od tego, czy planujemy podróż samochodem, spacerujemy do pracy czy biegamy na treningu. Dlatego tak istotne jest zrozumienie matematycznego wzoru, który pozwala nam obliczyć drogę pokonaną w czasie. W tym artykule przyjrzymy się bliżej temu zagadnieniu i rozwiążemy tajemnicę wzoru na drogę.
Czym jest wzór na drogę?
Wzór na drogę jest matematycznym narzędziem, które pomaga obliczyć odległość pokonaną przez obiekt w ruchu. Wartość ta może być używana w różnych kontekstach, od nauki fizyki po planowanie podróży. Wzór ten jest szczególnie przydatny, gdy znamy prędkość obiektu oraz czas podróży.
Wzór na drogę można zapisać następująco:
D=V⋅t
Gdzie:
- D to droga (odległość)
- V to prędkość
- t to czas podróży
Ten prosty wzór może okazać się niezwykle przydatny w wielu sytuacjach. Przyjrzyjmy się teraz, jak go używać w praktyce.
Przykłady zastosowań wzoru na drogę
Wzór na drogę można wykorzystać w wielu codziennych sytuacjach. Oto kilka przykładów:
- Podróż samochodem: Jeśli planujesz długą podróż samochodem i znasz średnią prędkość, jaką zamierzasz utrzymywać, oraz planowany czas podróży, możesz użyć wzoru na drogę, aby obliczyć przewidywaną odległość.
- Bieganie: Jeśli jesteś biegaczem i chcesz monitorować swoje postępy, możesz użyć wzoru na drogę, aby obliczyć, ile kilometrów przebiegłeś w określonym czasie.
- Nauka fizyki: Wzór na drogę jest również często wykorzystywany w nauczaniu fizyki. Uczniowie i studenci używają go do rozwiązywania problemów związanych z ruchem.
Tabela: Przykłady obliczeń za pomocą wzoru na drogę
| Przykład | Prędkość (V) [km/h] | Czas podróży (t) [h] | Obliczona droga (D) [km] |
|---|---|---|---|
| Podróż samochodem | 100 | 4 | 400 |
| Bieganie | 12 | 0.5 | 6 |
| Nauka fizyki | 20 | 2 | 40 |
Nagłówek 3: Przydatne warianty wzoru na drogę
Warto dodać, że istnieją różne warianty wzoru na drogę, które można stosować w zależności od sytuacji. Na przykład, jeśli prędkość nie jest stała i zmienia się w czasie, możemy użyć wzoru całkowego lub przybliżać wartość prędkości w danym momencie.
- Wzór całkowy: W przypadku zmiennej prędkości możemy obliczyć drogę, korzystając z wzoru całkowego:
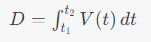
- Przybliżenie: Jeśli prędkość zmienia się w sposób nieregularny, możemy przybliżyć wartość prędkości w różnych punktach i użyć wzoru na drogę dla każdego z nich, a następnie zsumować wyniki.
Wzór na drogę jest narzędziem matematycznym, które znajduje szerokie zastosowanie w naszym codziennym życiu. Pomaga nam obliczać odległość pokonaną przez obiekty w ruchu i jest przydatny w wielu dziedzinach, od podróży po naukę fizyki. Dzięki prostemu wzorowi D=V⋅t oraz jego wariantom, możemy lepiej zrozumieć i kontrolować naszą przestrzeń i czas. Teraz, gdy znasz tajniki tego wzoru, możesz z niego korzystać w swoich codziennych obliczeniach i planach podróży.
